Lu Liu
Enhanced Verification of Safety and Security for Advanced Driver Assistance Systems
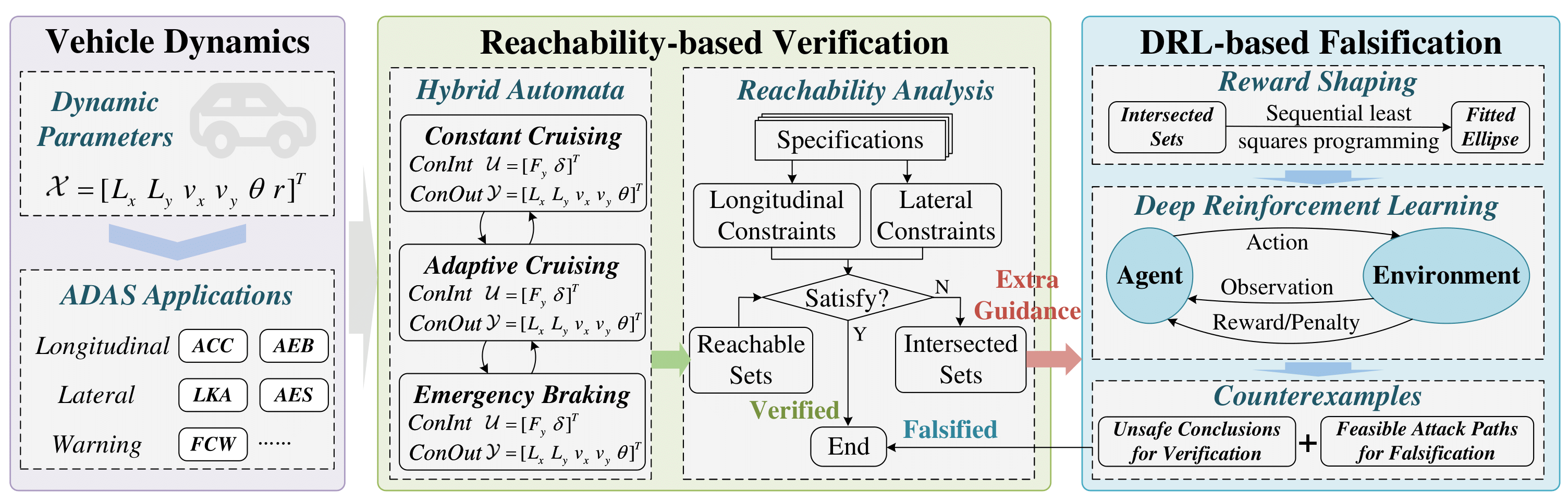
Code Available: https://github.com/liuluddex/Enhanced_Verification_Falsification
Hybrid Automaton Modeling
Vehicle Parameters
In our experiments, vehicle parameters are summarized in Tab. 1. These parameters are corresponding to simulator CarSim, and can be well used in vehicular behavior analysis. They are related to the motion of the vehicle and will be used in the ordinary differential equations (ODEs) that describe the vehicle’s motion. For example, when a vehicle is turning, both longitudinal and lateral accelerations are related to the vehicle quality. In addition, the other five parameters are also related to the vehicle’s steering movement and vary from vehicle to vehicle.
| Quality | Cornering Stiffness of Front Tires | Cornering Stiffness of Rear Tires | Distance between CG and Front Axle | Distance between CG and Rear Axle | Inertia of Z-axle | |
|---|---|---|---|---|---|---|
| Symbol | m | $(C_f$) | $(C_r$) | $(l_f$) | $(l_r$) | $(I_z$) |
| Unit | kg | N/rad | N/rad | m | m | - |
| Value | 1945 | 92064 | 92064 | 1.265 | 1.895 | 4095 |
Invariance of Discrete Modes
We study the dynamic behaviors between two vehicles and model it using a hybrid automaton. The hybrid automaton contains a total of 4 discrete modes, namely $q_1$ (CC), $q_2$ (ACC), $q_3$ (AEB), and $q_4$ (STOP). Each discrete mode has 6 scenarios $S_1 - S_6$, corresponding to different situations of the two vehicles turning. Tab. 2 illustrates the invariance of the discrete modes in the hybrid automaton. This invariance represents a combination of the mode-specific invariance and the scenario-based invariance. Invariance plays a crucial role in hybrid automata, as it determines whether a discrete mode can be sustained. If the current mode cannot be sustained, the system must transition to another mode based on the defined transition conditions.
| Mode | Scenario | Invariance |
|---|---|---|
| $(q_1$) (CC) | $(S_1$) | $(d_r \geq 75 \& L_{y_1} \leq d_1 \& L_{y_2} \leq d_1 \& \theta_1 = 0 \& \theta_2 = 0$) |
| $(S_2$) | $(d_r \geq 75 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_3$) | $(d_r \geq 75 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_4$) | $(d_r \geq 75 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_5$) | $(d_r \geq 75 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_6$) | $(d_r \geq 75 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(q_2$) (ACC) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \leq d_1 \& \theta_1 = 0 \& \theta_2 = 0$) |
| $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(q_3$) (AEB) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \leq d_1 \& \theta_1 = 0 \& \theta_2 = 0$) |
| $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -(d_r - 3) - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& -(d_r - 3) - 0.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(q_4$) (STOP) | $(S_1$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \leq d_1 \& L_{y_2} \leq d_1 \& \theta_1 = 0 \& \theta_2 = 0$) |
| $(S_2$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_3$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_1 = 0 \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_4$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | |
| $(S_5$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | |
| $(S_6$) | $(v_{y_1} \geq 1 \& d_r \geq 3 \& L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) |
Transition Relation
Tab. 3 shows the transition relation between different discrete modes of the hybrid automaton. Some are mode switches, others are scenario switches, and their corresponding conditions and resets are shown. It is necessary to specify both the source mode and scenario and the target mode and scenario. The core of the transition relation lies in condition and reset, one is the condition of transition, and the other is to reset certain state quantities during the transfer. Here, we study the dynamic behaviors of two vehicles on a single lane in a 90-degree turn scenario. Both vehicles have three different steering scenarios, which together give a total of six different scenarios. The switching of scenarios is related to the reset of $\delta$, which is crucial for steering. During state transitions, we reset $\delta$ and $r$. Similarly, during mode transitions, we reset $q$.
| Source Mode | Source Scenario | Target Mode | Target Scenario | Condition | Reset |
|---|---|---|---|---|---|
| $(q_1$) (CC) | $(S_1$) | $(q_1$) (CC) | $(S_2$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1$) | $(\delta_2' := 0.07, r_2' := 0$) |
| $(q_2$) (ACC) | $(S_1$) | $(q_2$) (ACC) | $(S_2$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1$) | $(\delta_2' := 0.07, r_2' := 0$) |
| $(q_3$) (AEB) | $(S_1$) | $(q_3$) (AEB) | $(S_2$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1$) | $(\delta_2' := 0.07, r_2' := 0$) |
| $(q_4$) (STOP) | $(S_1$) | $(q_4$) (STOP) | $(S_2$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1$) | $(\delta_2' := 0.07, r_2' := 0$) |
| $(q_1$) (CC) | $(S_2$) | $(q_1$) (CC) | $(S_3$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_2$) (ACC) | $(S_2$) | $(q_2$) (ACC) | $(S_3$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_3$) (AEB) | $(S_2$) | $(q_3$) (AEB) | $(S_3$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_4$) (STOP) | $(S_2$) | $(q_4$) (STOP) | $(S_3$) | $(L_{y_1} \leq d_1 \& L_{y_2} \geq d_1 \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_1$) (CC) | $(S_2$) | $(q_1$) (CC) | $(S_4$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_2$) (ACC) | $(S_2$) | $(q_2$) (ACC) | $(S_4$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_3$) (AEB) | $(S_2$) | $(q_3$) (AEB) | $(S_4$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_4$) (STOP) | $(S_2$) | $(q_4$) (STOP) | $(S_4$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \leq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_1$) (CC) | $(S_3$) | $(q_1$) (CC) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_2$) (ACC) | $(S_3$) | $(q_2$) (ACC) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_3$) (AEB) | $(S_3$) | $(q_3$) (AEB) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_4$) (STOP) | $(S_3$) | $(q_4$) (STOP) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0.07, r_1' := 0$) |
| $(q_1$) (CC) | $(S_4$) | $(q_1$) (CC) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_2$) (ACC) | $(S_4$) | $(q_2$) (ACC) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_3$) (AEB) | $(S_4$) | $(q_3$) (AEB) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_4$) (STOP) | $(S_4$) | $(q_4$) (STOP) | $(S_5$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \leq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_2' := 0, r_2' := 0$) |
| $(q_1$) (CC) | $(S_5$) | $(q_1$) (CC) | $(S_6$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0, r_1' := 0$) |
| $(q_2$) (ACC) | $(S_5$) | $(q_2$) (ACC) | $(S_6$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0, r_1' := 0$) |
| $(q_3$) (AEB) | $(S_5$) | $(q_3$) (AEB) | $(S_6$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0, r_1' := 0$) |
| $(q_4$) (STOP) | $(S_5$) | $(q_4$) (STOP) | $(S_6$) | $(L_{y_1} \geq d_1 \& L_{y_2} \geq d_1 \& \theta_1 \geq \frac{\pi}{2} \& \theta_2 \geq \frac{\pi}{2}$) | $(\delta_1' := 0, r_1' := 0$) |
| $(q_1$) (CC) | $(S_1$) | $(q_3$) (AEB) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_2$) | $(q_3$) (AEB) | $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_3$) | $(q_3$) (AEB) | $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_4$) | $(q_3$) (AEB) | $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_5$) | $(q_3$) (AEB) | $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_6$) | $(q_3$) (AEB) | $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 3$) |
| $(q_1$) (CC) | $(S_1$) | $(q_2$) (ACC) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_1$) (CC) | $(S_2$) | $(q_2$) (ACC) | $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_1$) (CC) | $(S_3$) | $(q_2$) (ACC) | $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_1$) (CC) | $(S_4$) | $(q_2$) (ACC) | $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_1$) (CC) | $(S_5$) | $(q_2$) (ACC) | $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_1$) (CC) | $(S_6$) | $(q_2$) (ACC) | $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 \cdot (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3 \& d_r \leq d_0$) | $(q' := 2$) |
| $(q_2$) (ACC) | $(S_1$) | $(q_3$) (AEB) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_2$) (ACC) | $(S_2$) | $(q_3$) (AEB) | $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_2$) (ACC) | $(S_3$) | $(q_3$) (AEB) | $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_2$) (ACC) | $(S_4$) | $(q_3$) (AEB) | $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_2$) (ACC) | $(S_5$) | $(q_3$) (AEB) | $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_2$) (ACC) | $(S_6$) | $(q_3$) (AEB) | $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 3$) |
| $(q_3$) (AEB) | $(S_1$) | $(q_2$) (ACC) | $(S_1$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_2$) | $(q_2$) (ACC) | $(S_2$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_3$) | $(q_2$) (ACC) | $(S_3$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_4$) | $(q_2$) (ACC) | $(S_4$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_5$) | $(q_2$) (ACC) | $(S_5$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_6$) | $(q_2$) (ACC) | $(S_6$) | $(v_{y_2} - v_{y_1} \leq 0 \& -d_r - 1.6 * (v_{y_2} - v_{y_1}) \leq 0 \& d_r \geq 3$) | $(q' := 2$) |
| $(q_3$) (AEB) | $(S_1$) | $(q_4$) (STOP) | $(S_1$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
| $(q_3$) (AEB) | $(S_2$) | $(q_4$) (STOP) | $(S_2$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
| $(q_3$) (AEB) | $(S_3$) | $(q_4$) (STOP) | $(S_3$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
| $(q_3$) (AEB) | $(S_4$) | $(q_4$) (STOP) | $(S_4$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
| $(q_3$) (AEB) | $(S_5$) | $(q_4$) (STOP) | $(S_5$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
| $(q_3$) (AEB) | $(S_6$) | $(q_4$) (STOP) | $(S_6$) | $(v_{y_1} \geq 0 \& -d_r - 0.6 * (v_{y_2} - v_{y_1}) \geq 0 \& d_r \geq 3$) | $(q' := 4$) |
So far, we have introduced and listed the core of hybrid automata in detail. Parameter values, invariance, and transition relations are crucial to hybrid automata. With these, we can build a hybrid automaton and conduct subsequent experimental analysis. The Flow* model under normal conditions is shown in normal.model. With Flow*, we can compute the reachable sets under a specified initial state set.
Normal Behavior Analysis
Tab. 4 shows the six initial state sets used for normal behavior analysis. These six initial state sets contain six different state transition routes. By setting the initial value of the state quantity, we can put the system in different modes at the beginning and control its mode transfer path to study whether the vehicle will collide in different scenarios.
| Set | Route | Bound | $(v_{x_1}$) | $(v_{y_1}$) | $(L_{x_1}$) | $(L_{y_1}$) | $(\theta_1$) | $(r_1$) | $(\delta_1$) | $(v_{x_2}$) | $(v_{y_2}$) | $(L_{x_2}$) | $(L_{y_2}$) | $(\theta_2$) | $(r_2$) | $(\delta_2$) | $(t$) | $(d_r$) | $(q$) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $(In_1$) | $(q_1$) | min | 0.00 | 17.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 98.00 | 1 |
| max | 0.00 | 17.01 | 0.00 | 0.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 98.00 | 1 | ||
| $(In_2$) | $(q_2$) | min | 0.00 | 17.00 | 0.00 | 48.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 50.00 | 1 |
| max | 0.00 | 17.01 | 0.00 | 48.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 50.00 | 1 | ||
| $(In_3$) | $(q_1$) -> $(q_2$) | min | 0.00 | 17.00 | 0.00 | 18.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 80.00 | 1 |
| max | 0.00 | 17.01 | 0.00 | 18.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 10.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 80.00 | 1 | ||
| $(In_4$) | $(q_3$) -> $(q_4$) | min | 0.00 | 19.99 | 0.00 | 84.10 | 0.00 | 0.00 | -1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.90 | 1 |
| max | 0.00 | 20.00 | 0.00 | 84.10 | 0.00 | 0.00 | 1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.90 | 1 | ||
| $(In_5$) | $(q_3$) -> $(q_2$) | min | 0.00 | 15.09 | 0.00 | 84.10 | 0.00 | 0.00 | -1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.90 | 1 |
| max | 0.00 | 15.10 | 0.00 | 84.10 | 0.00 | 0.00 | 1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.90 | 1 | ||
| $(In_6$) | $(q_3$) -> $(q_2$) -> $(q_3$) | min | 0.00 | 17.00 | 0.00 | 87.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 12.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 0.00 | 11.00 | 1 |
| $(q_3$) -> $(q_2$) | max | 0.00 | 17.01 | 0.00 | 87.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 12.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 0.00 | 11.00 | 1 |
Reachable Sets with Attacks
In order to further study the impact of attacks under this high-risk situation, we selected two different scenarios of $In_4$. To create this scenario, the initial TTC needs to be less than 1.6 and close to 0.6. Tab. 5 shows two different scenario settings and the range of attack intensity per unit time under the two attack strategies.
| Scenario | Transition | Bound | $(v_{x_1}$) | $(v_{y_1}$) | $(L_{x_1}$) | $(L_{y_1}$) | $(\theta_1$) | $(r_1$) | $(\delta_1$) | $(v_{x_2}$) | $(v_{y_2}$) | $(L_{x_2}$) | $(L_{y_2}$) | $(\theta_2$) | $(r_2$) | $(\delta_2$) | $(d_r$) | $(\omega_{d_r}$) | $(\omega_{v_{y_1}}$) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $(A_1$) | $(q_3$) -> $(q_4$) | min | 0.00 | 19.50 | 0.00 | 84.10 | 0.00 | 0.00 | -1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | -1e-9 | 13.90 | 0.00 | -2.40 |
| max | 0.00 | 20.00 | 0.00 | 84.10 | 0.00 | 0.00 | 1e-9 | 0.00 | 7.00 | 0.00 | 98.00 | 0.00 | 0.00 | 1e-9 | 13.90 | 1.80 | 0.00 | ||
| $(A_2$) | $(q_3$) -> $(q_4$) | min | -0.01 | 17.50 | 0.00 | 85.10 | 0.00 | 0.00 | -1e-9 | 0.00 | 5.00 | 0.00 | 99.00 | 0.00 | 0.00 | -1e-9 | 13.90 | 0.00 | -2.40 |
| max | 0.01 | 18.00 | 0.00 | 85.10 | 0.00 | 0.00 | 1e-9 | 0.00 | 5.00 | 0.00 | 99.00 | 0.00 | 0.00 | 1e-9 | 13.90 | 1.80 | 0.00 |
Tool Error Comparisons
Due to the falsification part, we use Python to implement a method based on deep reinforcement learning to find feasible attack paths, so we need to compare the error between the Python code implementation and Flow*. We compared the errors between the two code solutions under 27 different initial state sets, including root mean squared error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and mean square error (MSE). Tab. 3 shows 27 initial state sets and the corresponding errors between tools.
| Set | Bound | $(v_{x_1}$) | $(v_{y_1}$) | $(L_{x_1}$) | $(L_{y_1}$) | $(\theta_1$) | $(r_1$) | $(\delta_1$) | $(v_{x_2}$) | $(v_{y_2}$) | $(L_{x_2}$) | $(L_{y_2}$) | $(\theta_2$) | $(r_2$) | $(\delta_2$) | $(d_r$) | RMSE | MAE | MAPE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $(In_1$) | min | 0.00 | 16.36 | 0.00 | 88.21 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.97 | 0.00 | 98.8 | 0.00 | 0.00 | -1e-9 | 10.59 | 0.01 | 0.00 | 0.05 |
| max | 0.00 | 16.36 | 0.00 | 88.21 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.97 | 0.00 | 98.8 | 0.00 | 0.00 | 1e-9 | 10.59 | ||||
| $(In_2$) | min | 0.00 | 14.68 | 0.00 | 84.63 | 0.00 | 0.00 | -1e-9 | 0.00 | 3.62 | 0.00 | 99.0 | 0.00 | 0.00 | -1e-9 | 14.37 | 0.05 | 0.04 | 0.54 |
| max | 0.00 | 14.68 | 0.00 | 84.63 | 0.00 | 0.00 | 1e-9 | 0.00 | 3.62 | 0.00 | 99.0 | 0.00 | 0.00 | 1e-9 | 14.37 | ||||
| $(In_3$) | min | 0.00 | 11.29 | 0.00 | 86.58 | 0.00 | 0.00 | -1e-9 | 0.00 | 6.79 | 0.00 | 98.4 | 0.00 | 0.00 | -1e-9 | 11.82 | 0.01 | 0.01 | 0.09 |
| max | 0.00 | 11.29 | 0.00 | 86.58 | 0.00 | 0.00 | 1e-9 | 0.00 | 6.79 | 0.00 | 98.4 | 0.00 | 0.00 | 1e-9 | 11.82 | ||||
| $(In_4$) | min | 0.00 | 19.82 | 0.00 | 87.66 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.23 | 0.00 | 98.85 | 0.00 | 0.00 | -1e-9 | 11.19 | 0.01 | 0.01 | 0.10 |
| max | 0.00 | 19.82 | 0.00 | 87.66 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.23 | 0.00 | 98.85 | 0.00 | 0.00 | 1e-9 | 11.19 | ||||
| $(In_5$) | min | 0.00 | 14.89 | 0.00 | 80.88 | 0.00 | 0.00 | -1e-9 | 0.00 | 11.97 | 0.00 | 98.42 | 0.00 | 0.00 | -1e-9 | 17.54 | 0.01 | 0.00 | 0.03 |
| max | 0.00 | 14.89 | 0.00 | 80.88 | 0.00 | 0.00 | 1e-9 | 0.00 | 11.97 | 0.00 | 98.42 | 0.00 | 0.00 | 1e-9 | 17.54 | ||||
| $(In_6$) | min | 0.00 | 11.88 | 0.00 | 82.61 | 0.00 | 0.00 | -1e-9 | 0.00 | 4.35 | 0.00 | 98.9 | 0.00 | 0.00 | -1e-9 | 16.29 | 0.02 | 0.01 | 0.09 |
| max | 0.00 | 11.88 | 0.00 | 82.61 | 0.00 | 0.00 | 1e-9 | 0.00 | 4.35 | 0.00 | 98.9 | 0.00 | 0.00 | 1e-9 | 16.29 | ||||
| $(In_7$) | min | 0.00 | 18.11 | 0.00 | 82.61 | 0.00 | 0.00 | -1e-9 | 0.00 | 3.05 | 0.00 | 98.03 | 0.00 | 0.00 | -1e-9 | 15.42 | 0.07 | 0.06 | 0.93 |
| max | 0.00 | 18.11 | 0.00 | 82.61 | 0.00 | 0.00 | 1e-9 | 0.00 | 3.05 | 0.00 | 98.03 | 0.00 | 0.00 | 1e-9 | 15.42 | ||||
| $(In_8$) | min | 0.00 | 18.57 | 0.00 | 81.16 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.06 | 0.00 | 98.79 | 0.00 | 0.00 | -1e-9 | 17.63 | 0.01 | 0.01 | 0.07 |
| max | 0.00 | 18.57 | 0.00 | 81.16 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.06 | 0.00 | 98.79 | 0.00 | 0.00 | 1e-9 | 17.63 | ||||
| $(In_9$) | min | 0.00 | 17.16 | 0.00 | 79.95 | 0.00 | 0.00 | -1e-9 | 0.00 | 10.18 | 0.00 | 98.09 | 0.00 | 0.00 | -1e-9 | 18.14 | 0.02 | 0.01 | 0.08 |
| max | 0.00 | 17.16 | 0.00 | 79.95 | 0.00 | 0.00 | 1e-9 | 0.00 | 10.18 | 0.00 | 98.09 | 0.00 | 0.00 | 1e-9 | 18.14 | ||||
| $(In_{10}$) | min | 0.00 | 19.1 | 0.00 | 86.96 | 0.00 | 0.00 | -1e-9 | 0.00 | 14.3 | 0.00 | 98.45 | 0.00 | 0.00 | -1e-9 | 11.49 | 0.01 | 0.01 | 0.10 |
| max | 0.00 | 19.1 | 0.00 | 86.96 | 0.00 | 0.00 | 1e-9 | 0.00 | 14.3 | 0.00 | 98.45 | 0.00 | 0.00 | 1e-9 | 11.49 | ||||
| $(In_{11}$) | min | 0.00 | 15.1 | 0.00 | 79.5 | 0.00 | 0.00 | -1e-9 | 0.00 | 10.08 | 0.00 | 98.02 | 0.00 | 0.00 | -1e-9 | 18.52 | 0.01 | 0.01 | 0.06 |
| max | 0.00 | 15.1 | 0.00 | 79.5 | 0.00 | 0.00 | 1e-9 | 0.00 | 10.08 | 0.00 | 98.02 | 0.00 | 0.00 | 1e-9 | 18.52 | ||||
| $(In_{12}$) | min | 0.00 | 11.41 | 0.00 | 83.66 | 0.00 | 0.00 | -1e-9 | 0.00 | 6.32 | 0.00 | 99.0 | 0.00 | 0.00 | -1e-9 | 15.34 | 0.01 | 0.01 | 0.06 |
| max | 0.00 | 11.41 | 0.00 | 83.66 | 0.00 | 0.00 | 1e-9 | 0.00 | 6.32 | 0.00 | 99.0 | 0.00 | 0.00 | 1e-9 | 15.34 | ||||
| $(In_{13}$) | min | 0.00 | 15.07 | 0.00 | 78.85 | 0.00 | 0.00 | -1e-9 | 0.00 | 3.85 | 0.00 | 98.54 | 0.00 | 0.00 | -1e-9 | 19.69 | 0.02 | 0.02 | 0.16 |
| max | 0.00 | 15.07 | 0.00 | 78.85 | 0.00 | 0.00 | 1e-9 | 0.00 | 3.85 | 0.00 | 98.54 | 0.00 | 0.00 | 1e-9 | 19.69 | ||||
| $(In_{14}$) | min | 0.00 | 18.86 | 0.00 | 85.23 | 0.00 | 0.00 | -1e-9 | 0.00 | 4.24 | 0.00 | 98.48 | 0.00 | 0.00 | -1e-9 | 13.25 | 0.07 | 0.06 | 0.91 |
| max | 0.00 | 18.86 | 0.00 | 85.23 | 0.00 | 0.00 | 1e-9 | 0.00 | 4.24 | 0.00 | 98.48 | 0.00 | 0.00 | 1e-9 | 13.25 | ||||
| $(In_{15}$) | min | 0.00 | 11.93 | 0.00 | 81.99 | 0.00 | 0.00 | -1e-9 | 0.00 | 7.4 | 0.00 | 98.9 | 0.00 | 0.00 | -1e-9 | 16.91 | 0.01 | 0.01 | 0.04 |
| max | 0.00 | 11.93 | 0.00 | 81.99 | 0.00 | 0.00 | 1e-9 | 0.00 | 7.4 | 0.00 | 98.9 | 0.00 | 0.00 | 1e-9 | 16.91 | ||||
| $(In_{16}$) | min | 0.00 | 17.32 | 0.00 | 84.21 | 0.00 | 0.00 | -1e-9 | 0.00 | 9.88 | 0.00 | 98.48 | 0.00 | 0.00 | -1e-9 | 14.27 | 0.02 | 0.01 | 0.13 |
| max | 0.00 | 17.32 | 0.00 | 84.21 | 0.00 | 0.00 | 1e-9 | 0.00 | 9.88 | 0.00 | 98.48 | 0.00 | 0.00 | 1e-9 | 14.27 | ||||
| $(In_{17}$) | min | 0.00 | 16.89 | 0.00 | 78.55 | 0.00 | 0.00 | -1e-9 | 0.00 | 8.51 | 0.00 | 98.28 | 0.00 | 0.00 | -1e-9 | 19.73 | 0.02 | 0.01 | 0.10 |
| max | 0.00 | 16.89 | 0.00 | 78.55 | 0.00 | 0.00 | 1e-9 | 0.00 | 8.51 | 0.00 | 98.28 | 0.00 | 0.00 | 1e-9 | 19.73 | ||||
| $(In_{18}$) | min | 0.00 | 17.03 | 0.00 | 85.57 | 0.00 | 0.00 | -1e-9 | 0.00 | 13.5 | 0.00 | 98.82 | 0.00 | 0.00 | -1e-9 | 13.25 | 0.01 | 0.01 | 0.07 |
| max | 0.00 | 17.03 | 0.00 | 85.57 | 0.00 | 0.00 | 1e-9 | 0.00 | 13.5 | 0.00 | 98.82 | 0.00 | 0.00 | 1e-9 | 13.25 | ||||
| $(In_{19}$) | min | 0.00 | 13.44 | 0.00 | 81.57 | 0.00 | 0.00 | -1e-9 | 0.00 | 9.27 | 0.00 | 98.24 | 0.00 | 0.00 | -1e-9 | 16.67 | 0.01 | 0.00 | 0.03 |
| max | 0.00 | 13.44 | 0.00 | 81.57 | 0.00 | 0.00 | 1e-9 | 0.00 | 9.27 | 0.00 | 98.24 | 0.00 | 0.00 | 1e-9 | 16.67 | ||||
| $(In_{20}$) | min | 0.00 | 17.46 | 0.00 | 86.59 | 0.00 | 0.00 | -1e-9 | 0.00 | 3.93 | 0.00 | 98.7 | 0.00 | 0.00 | -1e-9 | 12.11 | 0.07 | 0.07 | 1.10 |
| max | 0.00 | 17.46 | 0.00 | 86.59 | 0.00 | 0.00 | 1e-9 | 0.00 | 3.93 | 0.00 | 98.7 | 0.00 | 0.00 | 1e-9 | 12.11 | ||||
| $(In_{21}$) | min | 0.00 | 16.16 | 0.00 | 83.6 | 0.00 | 0.00 | -1e-9 | 0.00 | 8.27 | 0.00 | 98.33 | 0.00 | 0.00 | -1e-9 | 14.73 | 0.02 | 0.01 | 0.14 |
| max | 0.00 | 16.16 | 0.00 | 83.6 | 0.00 | 0.00 | 1e-9 | 0.00 | 8.27 | 0.00 | 98.33 | 0.00 | 0.00 | 1e-9 | 14.73 | ||||
| $(In_{22}$) | min | 0.00 | 15.89 | 0.00 | 87.0 | 0.00 | 0.00 | -1e-9 | 0.00 | 12.46 | 0.00 | 98.33 | 0.00 | 0.00 | -1e-9 | 11.33 | 0.01 | 0.01 | 0.07 |
| max | 0.00 | 15.89 | 0.00 | 87.0 | 0.00 | 0.00 | 1e-9 | 0.00 | 12.46 | 0.00 | 98.33 | 0.00 | 0.00 | 1e-9 | 11.33 | ||||
| $(In_{23}$) | min | 0.00 | 11.74 | 0.00 | 87.97 | 0.00 | 0.00 | -1e-9 | 0.00 | 7.49 | 0.00 | 98.78 | 0.00 | 0.00 | -1e-9 | 10.81 | 0.01 | 0.01 | 0.08 |
| max | 0.00 | 11.74 | 0.00 | 87.97 | 0.00 | 0.00 | 1e-9 | 0.00 | 7.49 | 0.00 | 98.78 | 0.00 | 0.00 | 1e-9 | 10.81 | ||||
| $(In_{24}$) | min | 0.00 | 16.45 | 0.00 | 86.26 | 0.00 | 0.00 | -1e-9 | 0.00 | 3.28 | 0.00 | 98.82 | 0.00 | 0.00 | -1e-9 | 12.56 | 0.04 | 0.03 | 0.45 |
| max | 0.00 | 16.45 | 0.00 | 86.26 | 0.00 | 0.00 | 1e-9 | 0.00 | 3.28 | 0.00 | 98.82 | 0.00 | 0.00 | 1e-9 | 12.56 | ||||
| $(In_{25}$) | min | 0.00 | 13.35 | 0.00 | 83.94 | 0.00 | 0.00 | -1e-9 | 0.00 | 5.87 | 0.00 | 98.34 | 0.00 | 0.00 | -1e-9 | 14.4 | 0.01 | 0.01 | 0.09 |
| max | 0.00 | 13.35 | 0.00 | 83.94 | 0.00 | 0.00 | 1e-9 | 0.00 | 5.87 | 0.00 | 98.34 | 0.00 | 0.00 | 1e-9 | 14.4 | ||||
| $(In_{26}$) | min | 0.00 | 16.09 | 0.00 | 87.48 | 0.00 | 0.00 | -1e-9 | 0.00 | 9.35 | 0.00 | 98.07 | 0.00 | 0.00 | -1e-9 | 10.59 | 0.02 | 0.01 | 0.14 |
| max | 0.00 | 16.09 | 0.00 | 87.48 | 0.00 | 0.00 | 1e-9 | 0.00 | 9.35 | 0.00 | 98.07 | 0.00 | 0.00 | 1e-9 | 10.59 | ||||
| $(In_{27}$) | min | 0.00 | 11.73 | 0.00 | 86.32 | 0.00 | 0.00 | -1e-9 | 0.00 | 9.05 | 0.00 | 98.42 | 0.00 | 0.00 | -1e-9 | 12.1 | 0.00 | 0.00 | 0.03 |
| max | 0.00 | 11.73 | 0.00 | 86.32 | 0.00 | 0.00 | 1e-9 | 0.00 | 9.05 | 0.00 | 98.42 | 0.00 | 0.00 | 1e-9 | 12.1 |